An intro to Prisoner’s Dilemma

The first musings

I have recently been reworking a computer science and mathematics workshop that I have been running with the United Innovators , and I thought that I might as well share my thoughts on just how interesting I think it is.

What is Prisoner’s Dilemma?

Normal Prisoner’s Dilemma

Prisoner’s Dilemma is a classical game theory problem in which two prisoners are given the option to defect (betray the other) or cooperate (stay tight lipped). These actions carry different incentives depending on the actions of the opponent that can be represented like so:

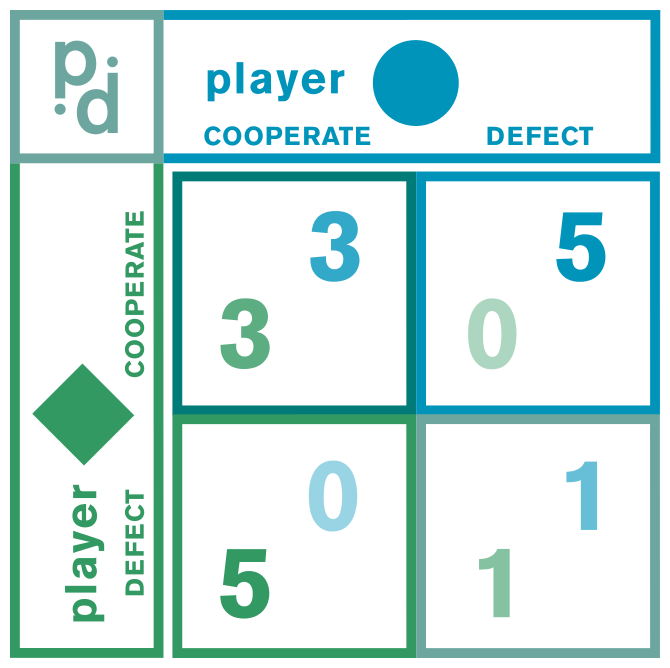
Thus, when playing a single game the best option is always to defect because it minimizes the potential cost while maximizing the potential reward, especially since the opponent cannot retaliate later.

Iterated Prisoner’s Dilemma

However, things get more interesting when we spice them up with a twist on the game, iterated prisoner’s dilemma. In this case, the players play multiple successive games, both aware of the other’s past moves. This means that there is a possibility for retaliation, creating a need for more nuanced strategies.

Through the Lens of Game Theory

Game theory is as Wikipedia puts,

The study of mathematical models of conflict and cooperation between intelligent rational decision-makers.” Wikipedia

In other words, it deals with how to maximize rewards and minimize negative outcomes when competing and cooperating with other selfish parties.

If we translate iterative prisoner’s dilemma into the terms of game theory, this means that we get a game that is:

Symmetrical

Both parties have equal power

Non-Zero Sum

Net result is not necessarily 0, so both players can win or lose

Simultaneous

Players make their moves simultaneously

Imperfect Information

Each player does not know what the other one is doing

Discrete Game

Moves are discrete and binary

Some History…

At this point I think that its interesting to inject some historical context into this problem.

Would you like to play a game?

Yes, I did just manage to tie this in with Wargames. Prisoner’s Dilemma actually does originate from the Cold War when the United States was struggling to figure out how to keep the Arms Race under control without over-escalating to war. Around the time of the Cuban Missile Crisis they came to an organization called the Rand Corporation, an American nonprofit global policy think tank made up of mathematicians, economists, and public policy experts. These academics subsequently modeled the scenario using the mathematical model of Prisoner’s Dilemma and made pioneering working studying this problem, all to avoid nuclear war (or win one when they thought it was possible to).

Axelrod’s Tournament

The Tournament

In the 80’s a professor named Robert Axelrod decided to try a new approach to Prisoner’s Dilemma. He setup a round robin tournament in which he excepted code submissions from around the world to compete as bots. The interesting thing is that he discovered that it is the “greedy” strategies, those that are the most selfish, that in the long run did the worst whereas within that scope it was the more altruistic strategies that began to shine. This lead him to conclude that cooperation between organisms might actually be the result of natural selection, with the most strictly selfish (over the short term) behaviors that in the end lead to failure.

So, which strategy won?

Tit for Tat

While it obviously depends on the competitors, the winner of the tournament was a remarkably short and simple strategy called Tit for Tat. The rules for it were simple:

1. Always start by cooperating
2. Repeat the same move the opponent did the move before In other words, this algorithm tries to quick start a virtuous cycle of cooperation, then rewards further cooperation from the opponent with cooperation and penalizes defections by retaliating with a defection. This avoids the costly situation of cooperating when the opponent defects, while still attempting to construct a virtuous cycle of mutual cooperation, the only move in the game that truly benefits both players.

Variants of Tit for Tat

Over the years, a couple of variants of Tit for Tat have emerged. Some like Two Tits for Tat are a little stricter when it comes to retaliation by retaliating with a defection for two turns instead of one, while others have introduced the concept of forgiveness, that the bot has a certain probability of cooperating even if the opponent defects.

My own strategy!

The entire concept of Prisoner’s Dilemma, the mix between geopolitics, mathematics, and computer science, fascinated me enough that not only have I run a workshop on it (and I’m planning on doing another one soon), but I actually came up with my own original strategy called Dynamic Two Tits for Tat which you can take a closer look at in my portfolio here . In fact, if you want to take a closer look, it is now a strategy integrated into the Axelrod repository, an awesome open source project that you can take a look at here, and which allows you to run full blown matches and tournaments between strategies (and so much more)!

I digress. My own minor contribution to this field is another variant of Tit for Tat. It is actually based off of Two Tits for Tat, but integrates a probability of forgiveness, meaning cooperating even when the opponent has defected within the last two turns, which is calculated as the ration of the opponents number of defections and total number of moves:

This represents in a sense just how nice the opponent is, and thus allows my bot to determine how forgiving it should be of its opponent based off of this (which is also the odds that any move by the opponent will be a defection).

The Only Way to Win is Not to Play…

Or maybe just to outsmart them with a better strategy (just kidding, nuclear war is unwinnable).

And on that bright note, I hope you enjoyed my write up on the Prisoner’s Dilemma. I can’t encourage you enough to check out the Axelrod repository here, or even my portfolio section on my strategy here if this interests you.

Dr. Strangelove: The whole point of the doomsday machine is lost…if you keep it a secret! Why didn’t you tell the world, eh?! Russian Ambassador: It was to be announced at the Party Congress on Monday. As you know, the Premier loves surprises. Dr. Strangelove: Or How I Learned to Stop Worrying and Love the Bomb