A Little bit of Context
For a workshop I ran as part of the United Innovators project (check out the rest of my portfolio for more information on that), I had the students conceptualize and then implement strategies to solve Iterated Prisoner’s Dilemma (click here to see my write up on Prisoner’s Dilemma). However, whenever I run an exercise like that, I always try to solve it myself first, and over the course of doing so I actually developed an original strategy for the problem, something that I honestly just find cool enough that I felt like putting it here (it is my portfolio after all).
A Twist on an Age Old Classic
Tit for Tat
My strategy is a new twist on the now classic Tit for Tat strategy which kicks off the match by cooperating and then simply copies the opponents previous move in order to incentise cooperation and punish defection, effectively pushing towards the only mutually beneficial action of both cooperating while trying to avoid the worst case scenario of cooperating when the opponent defects (if you have no clue what this means, I once again encourage you to read through my write up on Prisoner’s Dilemma here before you continue reading).
Dynamic Two Tits for Tat
Two flaws
However, whereas the traditional Tit for Tat only looks one move back to decide on its move, mine is based upon one of its variants, Two Tits for Tat, which as you may have guess punishes the opponent for defections within the last two turns.
However, vanilla Tit for Tat and its cousin Two Tits for Tat both have problems.
- In Tit for Tat’s case, it is pretty vulnerable to stochastic (random) strategies that have no rational logic that Tit for Tat can use to promote mutual cooperation.
- In Two Tits for Tat’s case, its longer memory can lead to a vicious cycle of defections.
Forgiveness to the rescue!
My new strategy, called Dynamic Two Tits for Tat, addresses these deficiencies by incorporating the idea of forgiveness into the Two Tits for Tat strategy. In other words, Dynamic Two Tits for Tat always has a probability that it will cooperate with the opponent, even if it defected within the last 2 turns. This probability as the ration of the opponents number of defections and total number of moves: 
.
This represents in a sense just how nice the opponent is, and thus allows my bot to determine how forgiving it should be of its opponent based off of this (which is also the odds that any move by the opponent will be a defection).
This forgiveness effectively allows my bot to avoid for the most part entering long, vicious cycles of defection by both sides (unless they really deserve it), while still allowing the bot to maintain a “willingness” to retaliate when necessary.
Enough words, it is time for some good looking graphs:
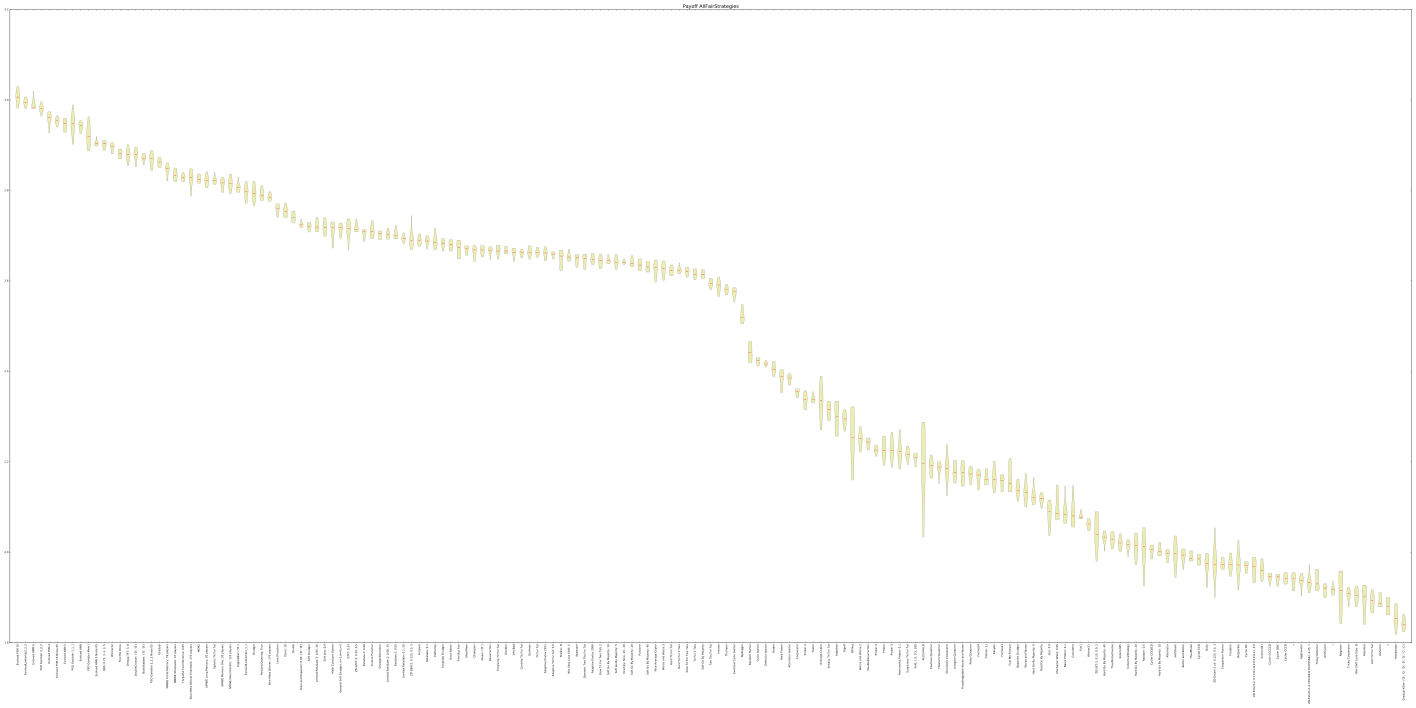
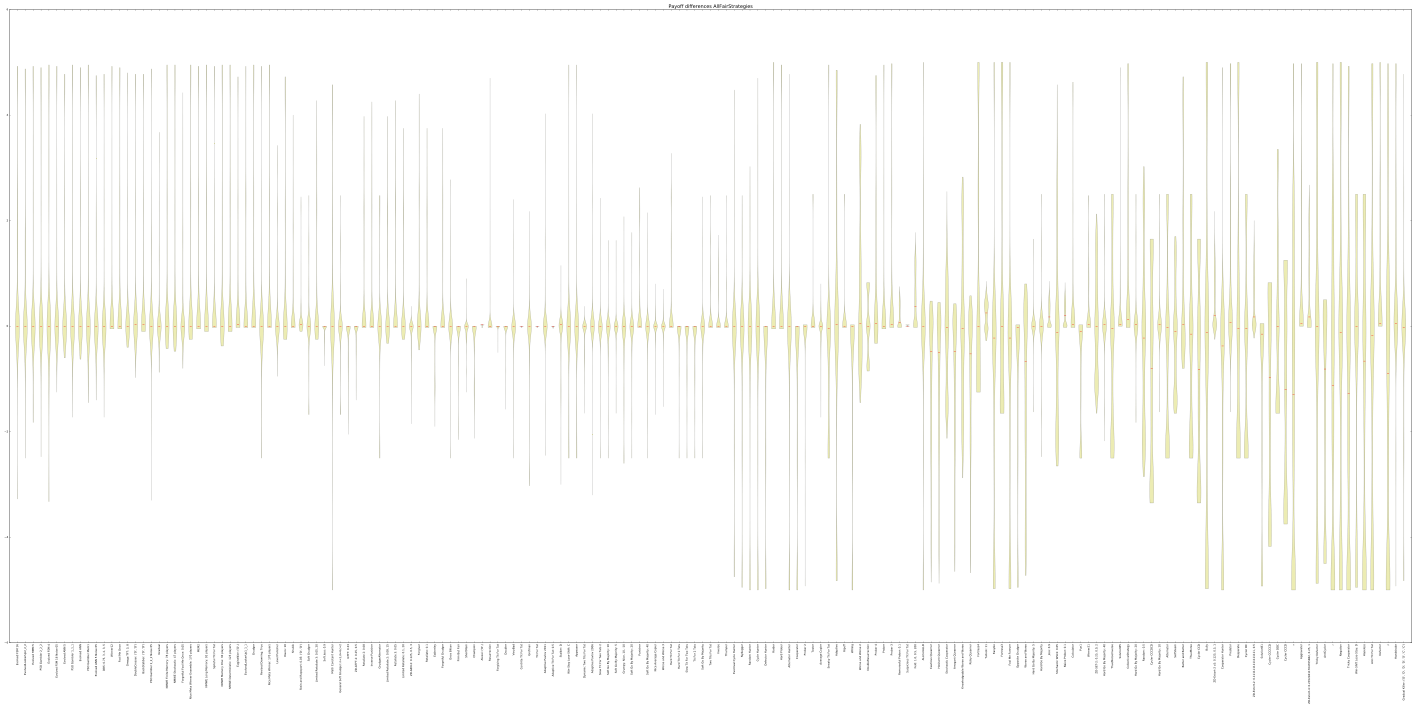
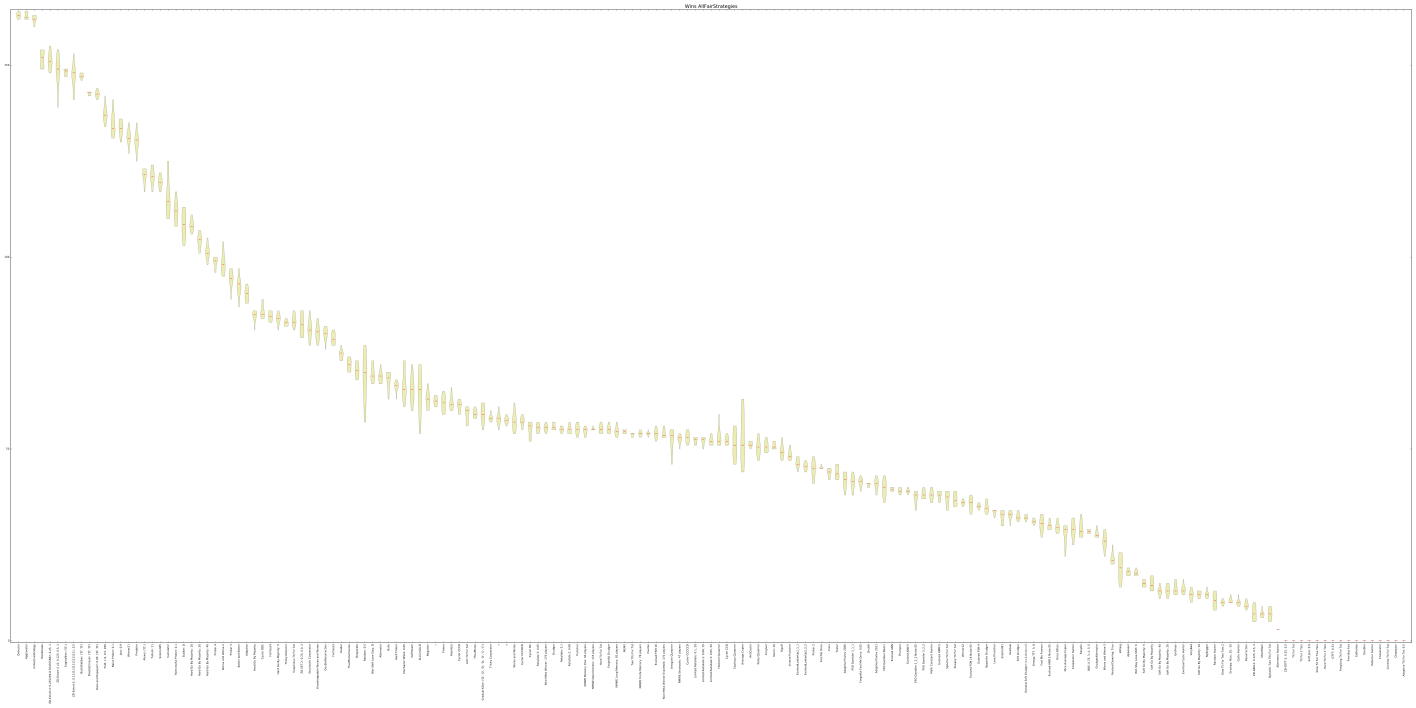
Awards
None, except that this strategy made its way into an actual academic research tool, something that I confess I am pretty proud of. You can take a look at the project’s Github page here .